How Linear Functions Can Be Parallel or Perpendicular

In the linear function formula: y = mx + b, linear functions will either be parallel or perpendicular to each other depending on the values of the variables m & b.

Changing the value of b will make the next function parallel to the original function you chose.

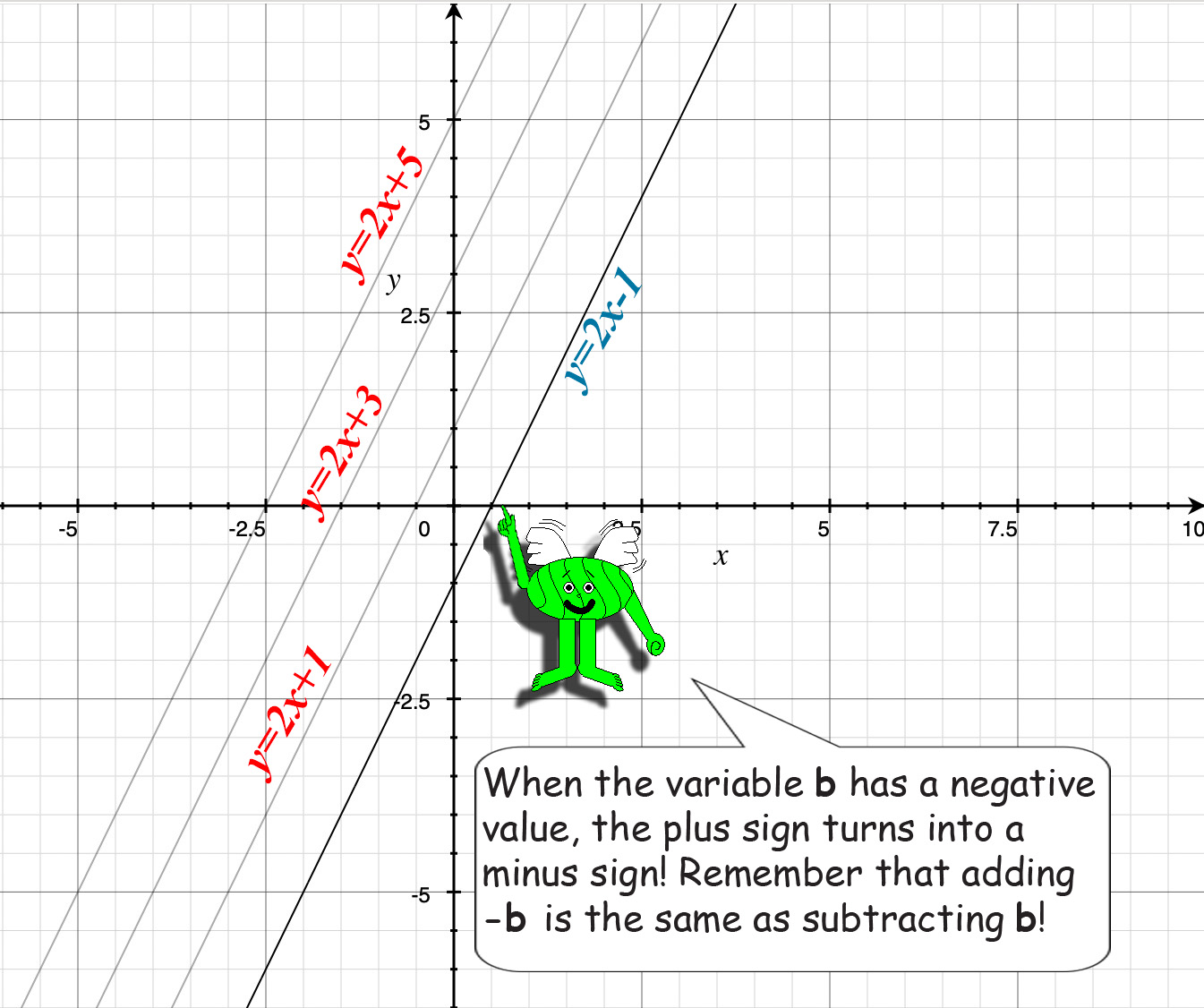
Multiplying the value of m or x by -1 will make the next function perpendicular to the original function you chose.

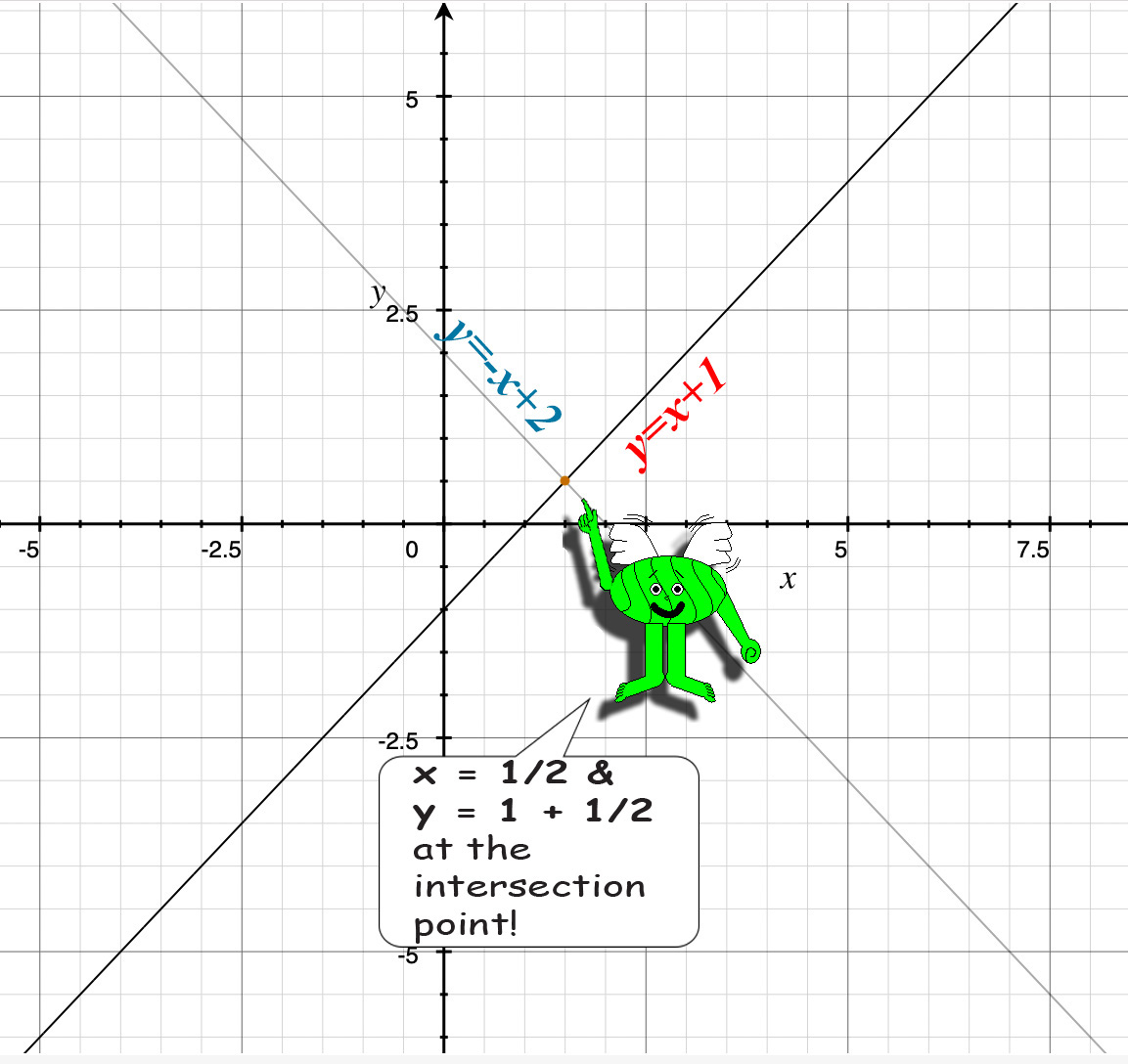
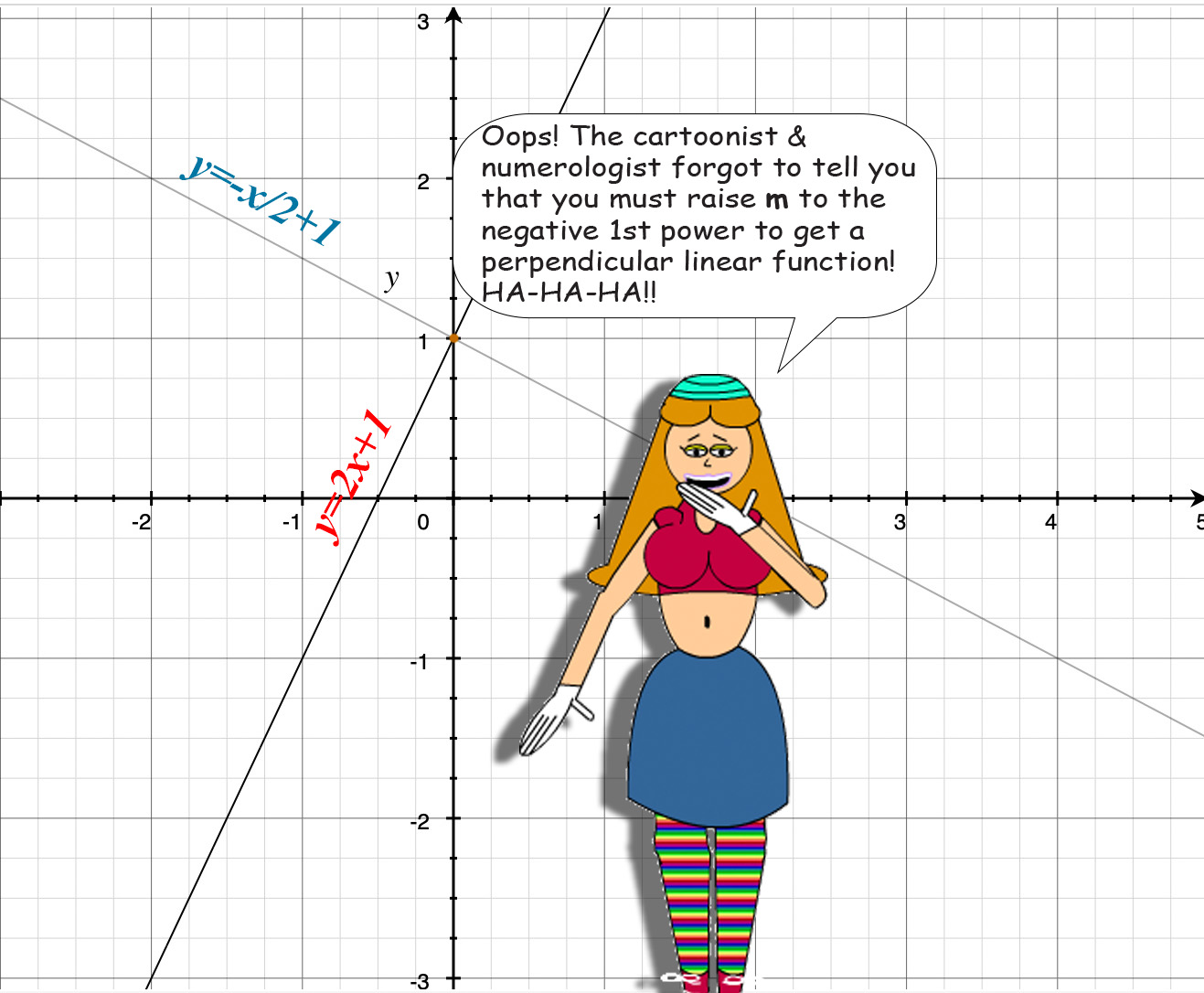
m must also be raised to the power of -1. Sorry I forgot to mention that!

However, changing the value of m changes the slope of the function. If lines intersect but don't make right angles, (which are 90 degrees) then it doesn't count as being perpendicular.

Conclusively, parallel linear functions never intersect! So:

x ≠ x + 1 ≠ x + 2 ≠ x + 3 ≠ etc.

x ≠ x - 1 ≠ x - 2 ≠ x - 3 ≠ etc.

No matter what the value of the variable is, x can NEVER be equal to x ± b, unless b is equal to zero(0) because zero(0) is the number of additive identity.

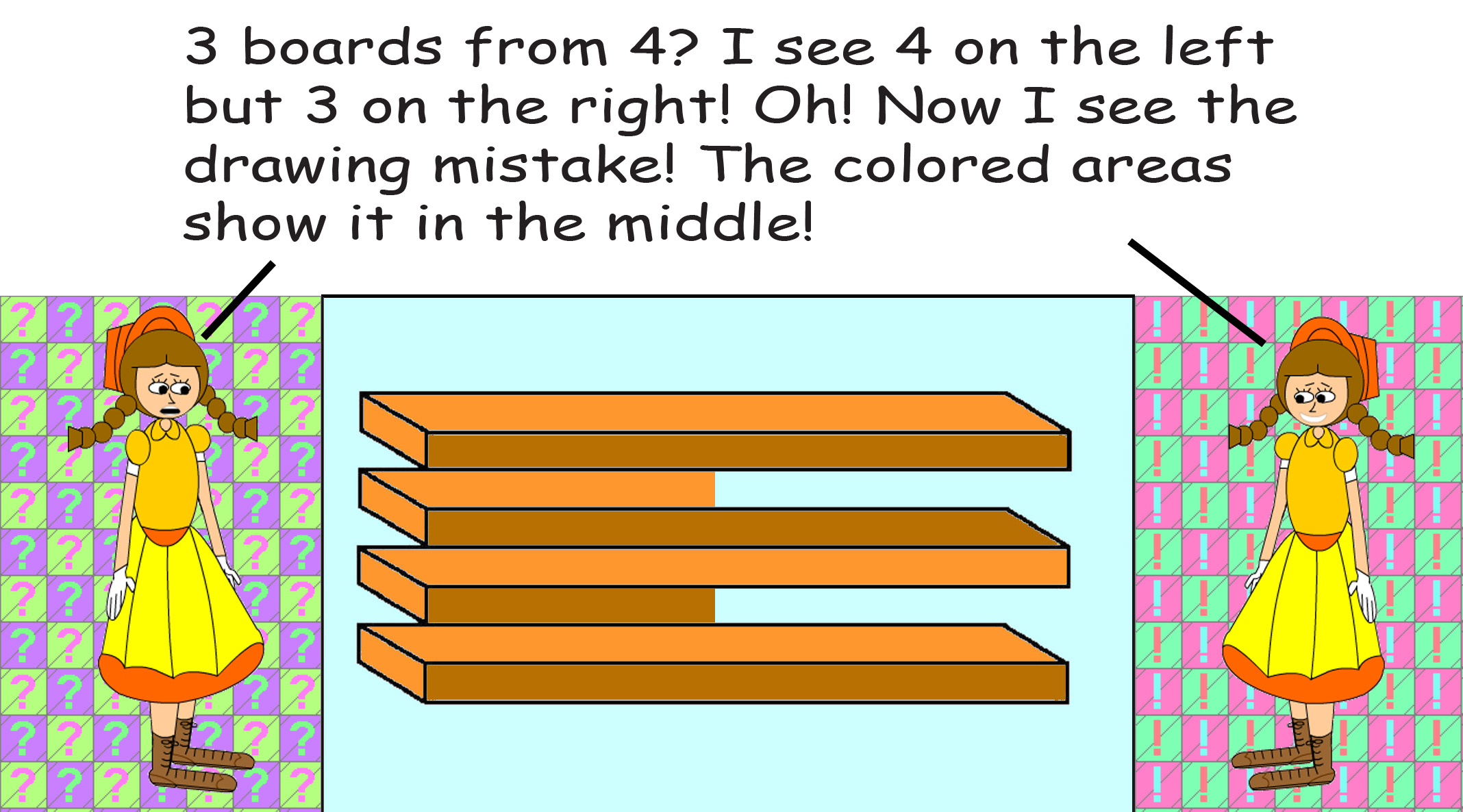
Finally, about lines, when it comes to drawing, make sure that you line up your outlines correctly or you might accidentally draw an impossible 3-D figure!

Back to Index Page Back to Math Trick Menu