

What Sally Brittany Martin(of the Photonese Martins) said to Burger Meat Food is correct. You can't win every game you play because perfection is unattainable basically. The only way to win 100% of the time is to win every single game that you play! But if you lose just 1 single game, then your win percentage drops below 100% & will never return back to 100% EVER! Why not? Well, below is my win percentage formula:

Observe the graph below. Notice how the curve changes when the value for L changes:
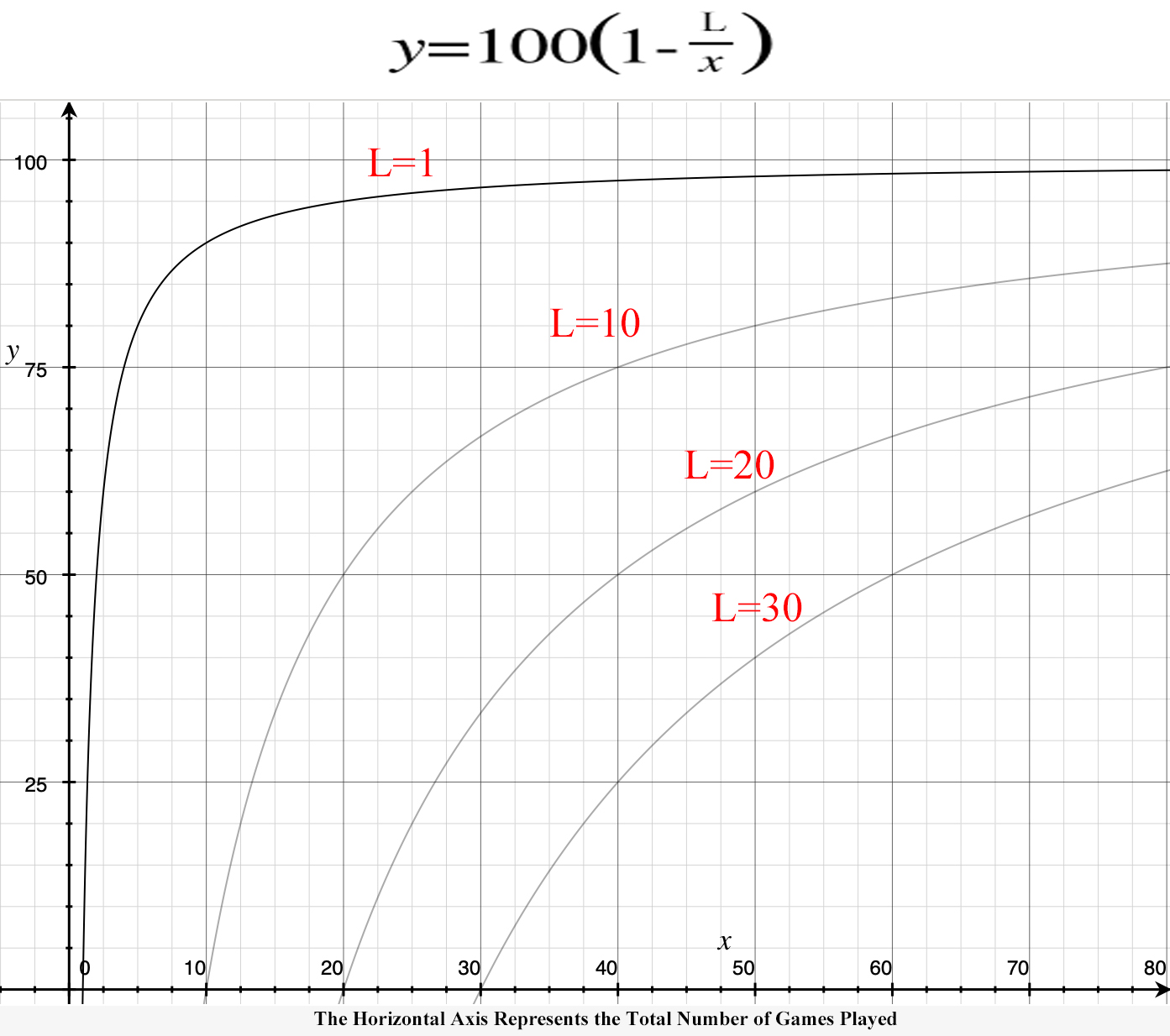
If L > x, then y would have a negative(or sub-zero) value, which would make an improbable case! (Probability only makes sense in Quadrant 1, where both x & y have positive values.) Also, L must be equal to a whole number. By the way, zero(0) counts as a whole number!

As you lose more games, the curve of the function moves away from the ultimate asymptote, which is 100. If L was equal to zero(0), then the function will become the constant y = 100 by simplification. That means that so far, you won every game that you have played. (Hence, 100% would be your win percentage.) In order for it to stay that way, you would have to keep winning every single game you play afterwards; otherwise, it's no longer 100%; it becomes less than 100% & stays that way forevermore! To prevent your win percentage from going below 100%, you would have to quit playing more games before losing even just ONCE!
But why would you quit playing games altogether if you enjoy playing them? 1 thing that seems to say "Game Over Permanently" is death itself since you'd no longer be alive to play more games. However, when the resurrection time in the future eventually comes, it'll remove the adverb "Permanently"! (Get the joke & how I used the word "Permanently" in the 2 previous sentences?)
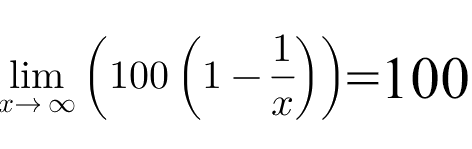

Back to Index Page Back to Math Trick Menu
© Derek Cumberbatch