Invincible Integration 2!

(n ≥ 1)

When the variable n is equal to a natural number, you get a fraction in which the numerator is 1 less than the denominator!

According to the Power Rule, the integral of the function pictured above is:

-1/x + C

(The C is there to remind us that the derivative of any constant is zero(0) & that the derivative of the function will remain the same no matter what the constant is!)

Miss Zero representing the number zero(0) again!

So, for example, if n = 8, then (n - 1)/n = 7/8. As you compute the boundaries, you'll have to add -1/8 to 1, which gives you 7/8.

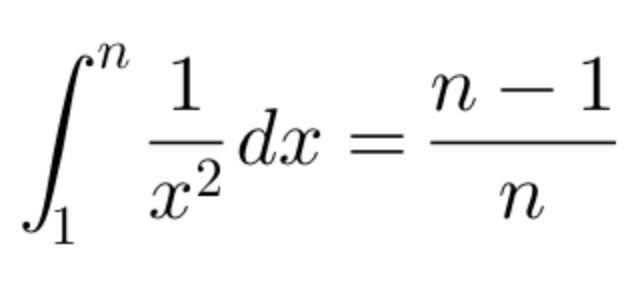
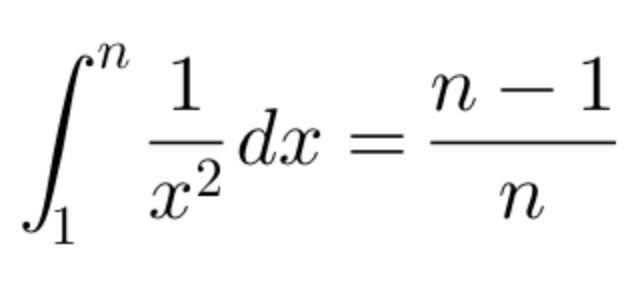
Here's the graph just below:

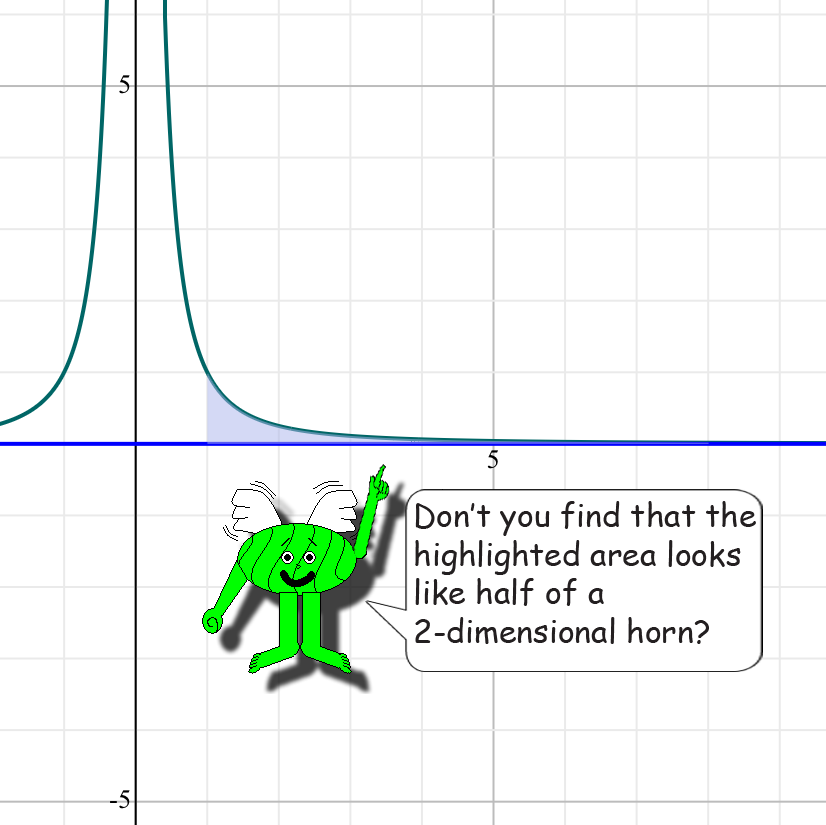
You may have heard of Gabriel's Horn, which is an imaginary horn of infinite length based on this special function: y = 1/x². To calculate its volume, simply multiply the integral by pi(π). However, n = ∞ due to this imaginary horn being infinitely long! Its surface area is also infinite! In fact, this horn is too big to fit into the physical universe! Anyway, this Web page is about the 2-dimensional version of this imaginary horn. (Or at least half of it!)

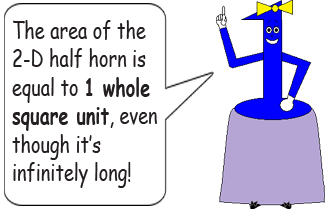
In the example, we calculated part of the area of the 2-D half horn. (From x = 1 to x = 8)

Also, to conclude this Web page, you can also print the function as: y = x^-2

Back to Index Page Back to Math Trick Menu