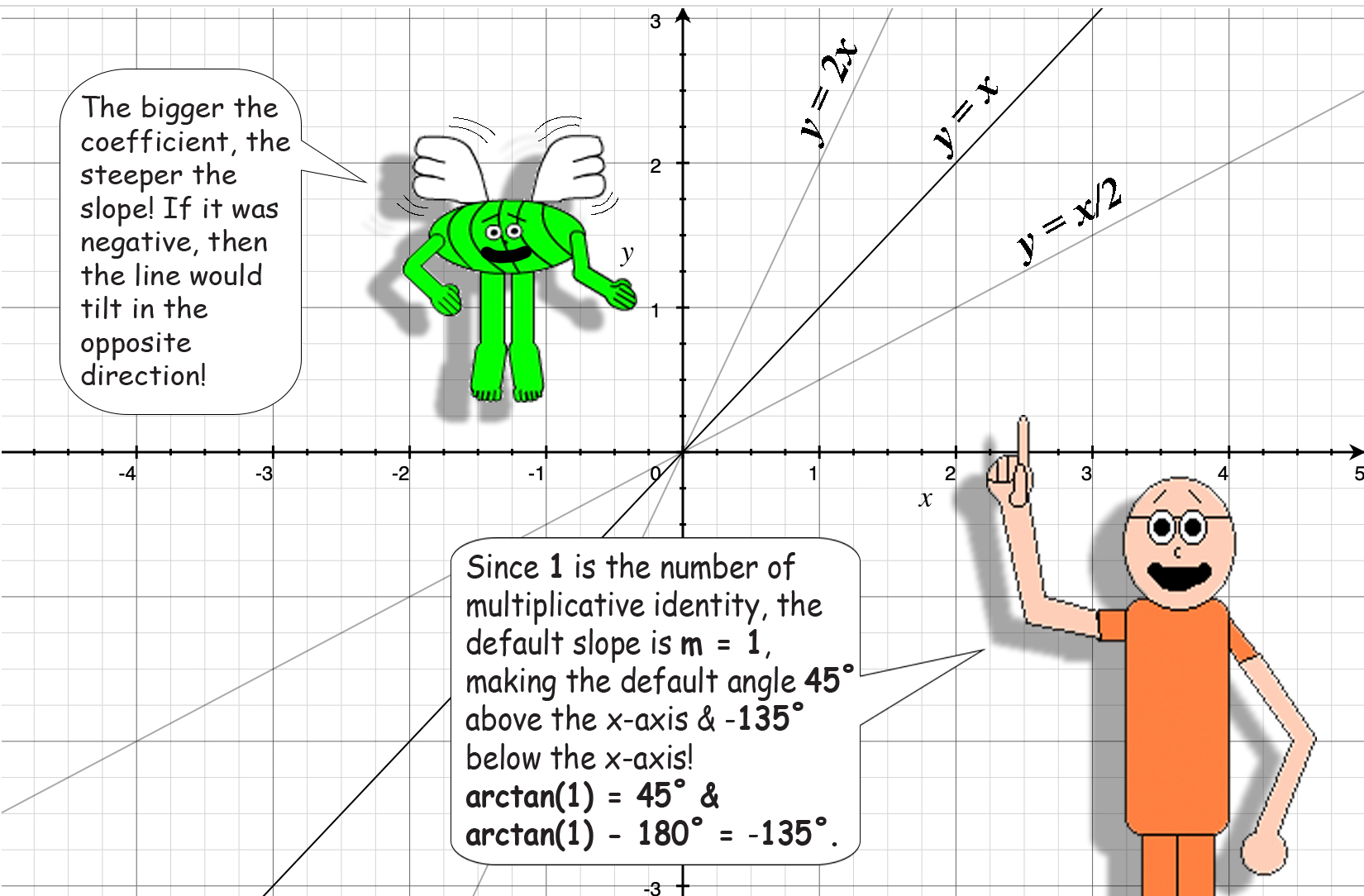
In functions, the number that the variable x is multiplied by is called the coefficient. This number effects the slope of linear functions. In fact, the coefficient is EQUAL to the slope! The slope determines the angle that the function intersects the x-axis by. Linear functions are in the form: y = mx + b where y is the dependent variable, m is the slope, x is the independent variable & b is the constant addend. (Note: When b is negative, the plus turns into a minus!) There's a formula for the angle that the function intersects the x-axis by for each quadrant; however, a linear function can only cross up to 2 quadrants at a time when b = 0; if m is positive, then it'll cross Quadrants I & III, but if m is negative, then it'll cross Quadrants II & IV. It ALWAYS passes thru the origin point when b = 0.
If b = 0 in a linear function, then the angle that it crosses the x-axis by is equal to:
arctan(m) in Quadrant I
arctan(m) + 180° in Quadrant II
arctan(m) - 180° in Quadrant III
arctan(m) in Quadrant IV
And remember, m is the slope of the linear function!
I almost forgot: In function graphs, the angles of linear functions are measured in reference to the origin point & the right side of the x-axis so positive angles go counterclockwise & negative ones go clockwise.

The angle of y = 2x above the x-axis is 63° 26' 5.816" (The apostrophe stands for arcminutes & the quotation mark stands for arcseconds.)
The angle of y = 2x below the x-axis is -116° 33' 54.184"
The angle of y = x/2 above the x-axis is 26° 33' 54.184"
The angle of y = x/2 below the x-axis is -153° 26' 5.816"
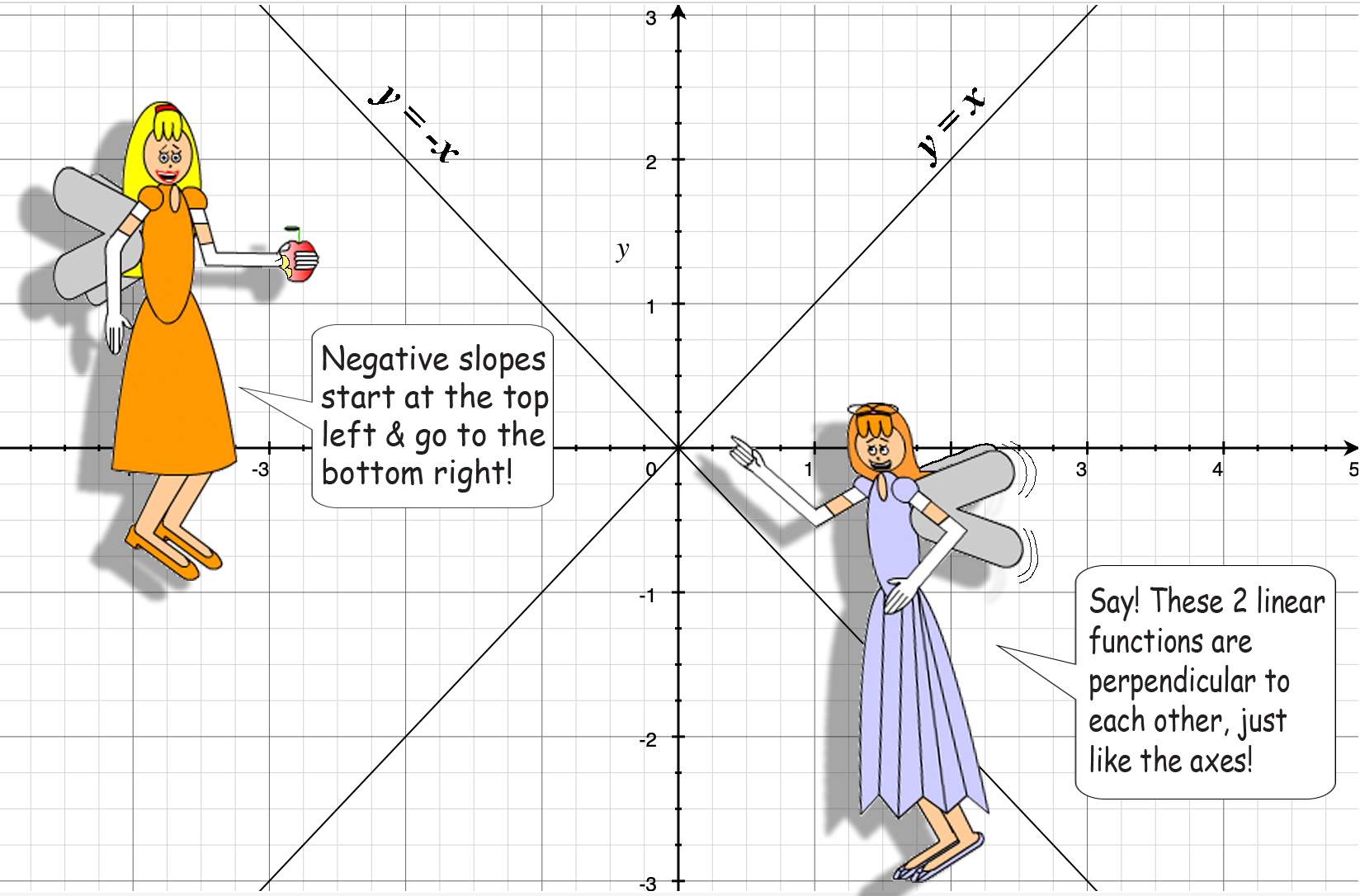
Dr. John Von Foolish already told us what the angles of y = x are above & below the x-axis. The angle of y = -x is 135° above the x-axis & the angle below is -45°. Since Faye Pixie mentioned that these linear functions are perpendicular, you can tell that linear functions are perpendicular to each other indeed by knowing that perpendicular linear functions have slopes that are negative reciprocals of each other. For example, y = 5x & y = -x/5 have slopes that are negative reciprocals of each other, which makes them perpendicular to each other! (Note: Changing the value of b in at least 1 function will make them intersect at a different point!)
What happens if m = 0, you ask? Well, then the linear function becomes the constant function y = 0. The slope is zero(0) so the angle will be 0° on the right side of the y-axis & ±180° on the left of the y-axis. (Yes, I'm referring to the y-axis instead of the x-axis this time since this constant function collides with the x-axis. Also, I used the plus-minus(±) sign this time since 180-degree rotations always correspond to each other whether you go clockwise or counterclockwise!) Finally, changing the value of b in this case just slides the horizontal constant function upward if you make the value positive & downward if you make it negative.
Ever notice how quadratic functions can look like smiles or frowns? Quadratic functions are in the form: y = ax2 + bx + c. If a is positive, you get a "smile"! If a is negative, you get a "frown"! Coincidentally, positivity makes people smile & negativity makes people frown! Quadratic functions are always symmetrical through some vertical line that crosses the x-axis. You can find out which one by using this formula pictured below:

In the example shown below, notice how the parabola goes from "smile" to "frown" when the variable a becomes negative:
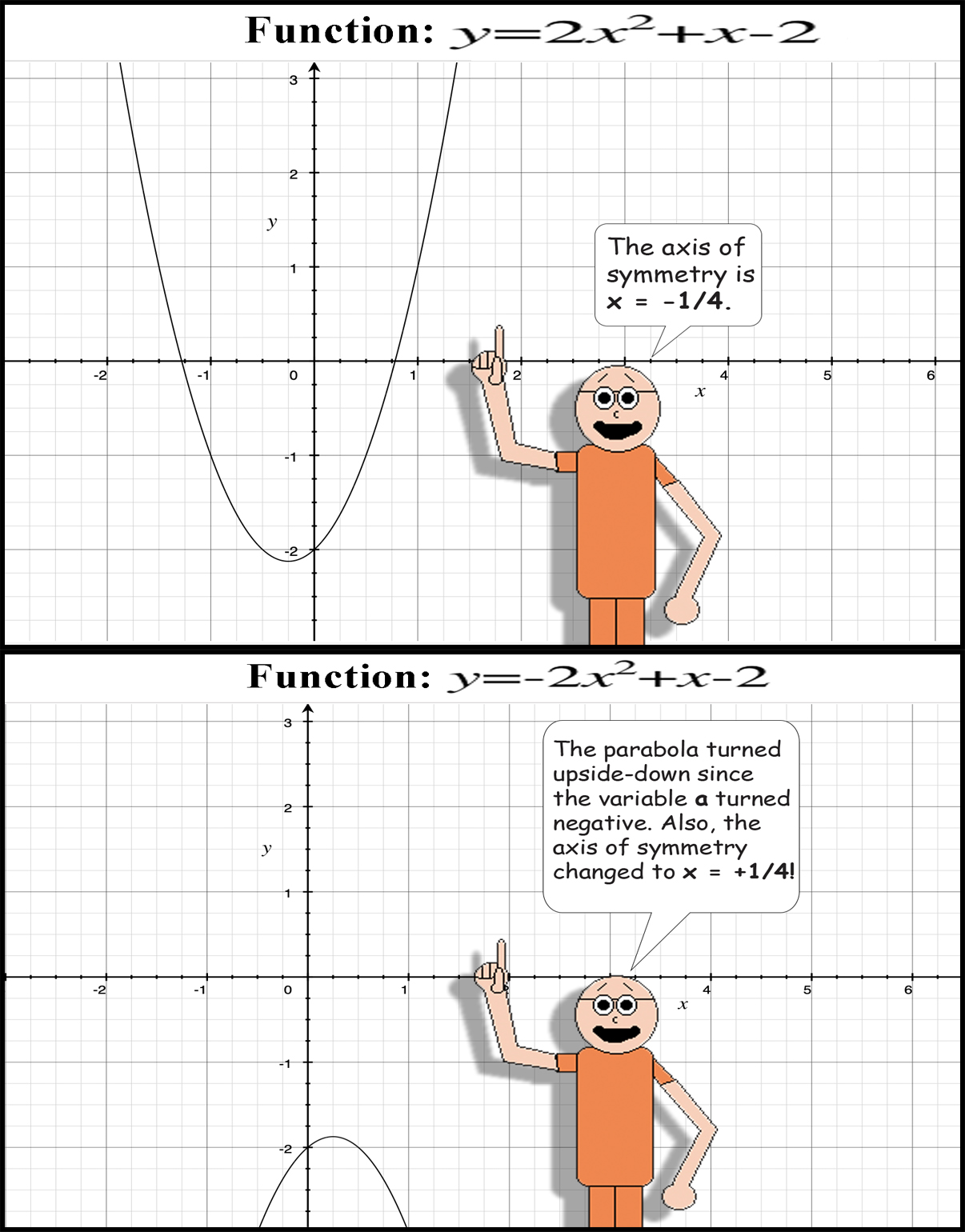
Finally, as this Web page concludes, the quadratic function is likely to intersect the x-axis if b ≠ 0, unless both a & c are either both positive or both negative. When a quadratic function doesn't intersect the x-axis, the only way that y can be equal to zero is if x is equal to the right imaginary or complex number! The axis of symmetry is always x = 0 if b = 0.

Back to Index Page Back to Math Trick Menu
© Derek Cumberbatch