Complex Number Kookiness 7

Observe the table below. Can you find something interesting in any 1 of the 2 columns?

The fraction ½ is added to consecutive integers multiplied by the imaginary unit i in the left column so that the squares of the absolute values of the complex numbers are equal to the squares of the consecutive integers + ¼! If the real & imaginary parts of the complex numbers swapped values, then their absolute values would stay exactly the same! The signs of the real part & imaginary part of each complex number doesn't matter because that won't change the absolute value!

Below is a copy of the 1st table, except that this time, I printed the conjugates of the complex numbers!

The main difference between a complex number & its conjugate is that the plus sign in the middle becomes a minus; or if it's already a minus, it becomes a plus!

Here are the conjugates of the ones for the 2nd table:

By the way, |a+bi| = |a-bi| = |-a+bi| = |-a-bi|; all 4 of those are exactly the same!(In absolute value) You can have the variables a & b swap places without changing the absolute value!

The absolute value of a complex number:

Finally, here's the appropriate formula for this math trick:

|½ ± Ni|² = |N ± ½i|² = N² + ¼

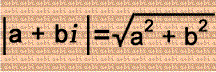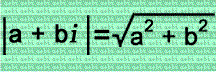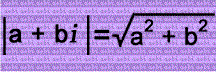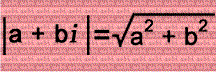
Back to Index Page Back to Math Trick Menu

© Derek Cumberbatch