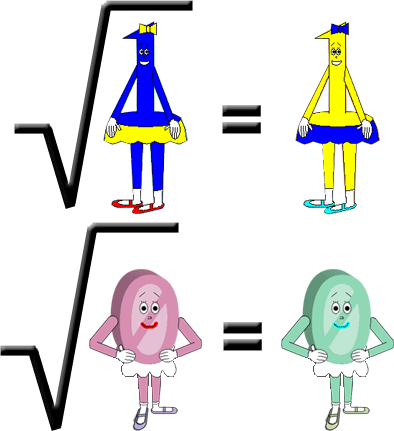Complex Number Kookiness 10
|√(x) + i| = √(x + 1)
|1 + i√(x)| = √(x + 1)
If the real or imaginary part of a complex number is equal to the square root of an integer & the other part is equal to 1, then the absolute value
of the complex number is equal to the square root of the binomial (x + 1)!

Remember this picture from "Complex Number Kookiness 9"?
Here comes the 1st table of complex numbers!
| Complex Numbers | Absolute Value |
| 1 + i√(0) | √(1) |
| 1 + i√(1) | √(2) |
| 1 + i√(2) | √(3) |
| 1 + i√(3) | √(4) (or 2) |
| 1 + 2i | √(5) |
| 1 + i√(5) | √(6) |
| 1 + i√(6) | √(7) |
| 1 + i√(7) | √(8) |
| 1 + i√(8) | √(9) (or 3) |
| 1 + 3i | √(10) |

As you may already know, 0, 1, 4, & 9 are the 4 integers mentioned in this table that are perfect squares. The 1st 2 are idempotent.
In this 2nd table, the real & imaginary parts of the complex numbers switch values! And...
| Complex Numbers | Absolute Value |
| 0 + i | 1 |
| 1 + i | √(2) |
| √(2) + i | √(3) |
| √(3) + i | √(4) (or 2) |
| 2 + i | √(5) |
| √(5) + i | √(6) |
| √(6) + i | √(7) |
| √(7) + i | √(8) |
| √(8) + i | √(9) (or 3) |
| 3 + i | √(10) |
Voila! We get the exact same old absolute values in the same order! (Noticed that I removed the radical signs from 1 & 0 at the top of this one.)
1 Warning: x must be equal to a positive integer or things will get screwy in the equation! When x is equal to a negative integer,
|√(x) + i| & |1 + i√(x)| will NOT be equal!
|1 + i√(-1)| = 0; |√(-1) + i| = 2
0 = 2 (This is a false statement!)
So, |1 + i√(-1)| ≠ |√(-1) + i|

Back to Index Page Back to Math Trick Menu
© Derek Cumberbatch